2.2. Numerical methods and the Underworld code¶
When the font of analysis is exhausted, numerical solutions become indispensable. Though the construction of robust and accurate systems for the computation of mantle convection problems is far from trivial, many successful approaches have been developed over the years, each with its own advantages and limitations. For this thesis we adopt a finite-element approach, which has been extensively developed by many groups over more than a quarter of a century. In particular, we follow after Professor Moresi and colleagues, the developers of modelling codes including CITCOM, Ellipsis, and most lately Underworld [Beucher et al., 2019, Farrington et al., 2005, May and Moresi, 2008, Moresi et al., 2003, Moresi et al., 2002, Moresi et al., 2007, Moresi and Solomatov, 1995, Moresi et al., 1996, Zhong et al., 1998].
Here we will discuss in broad terms the principles and infrastructure of our numerical modelling practice; particulars of model design and construction will be discussed in further chapters as relevance dictates.
2.2.1. Numerical methods¶
To take a numerical approach to mantle convection is to endeavour to iteratively solve the following system of equations, which are the Stokes, conservation, and advection-diffusion equations under the assumptions of incompressibility and infinite Prandtl number:
Where \(\eta\) is dynamic viscosity, \(D\) the strain rate tensor, \(p\) dynamic pressure, \(\Delta\rho\) the density anomaly, \(g\) the gravity vector, \(\overline{u}\) the velocity vector, \(T\) temperature, \(\kappa\) thermal diffusivity, \(t\) time, and \(H\) a thermal source term, i.e. radiogenic heating.
The first two equations together solve for velocity given buoyancy and viscosity without accounting for inertia (hence the lack of time-dependency), while the third equation governs determines the change in temperature at any given point after an infinitesimal time interval due to diffusion (the first term) and advection (the second). Temperature, being the only time-dependent quantity, is the only necessary variable of state for this system. It is further possible to construct the viscosity and diffusivity parameters as functions of space, time, temperature, velocity, et cetera, to achieve much more complex rheologies as desired; plastic, elastic, rigid, and insulating materials may all be implemented in this way, each with its own perils and caveats.
We have already established that the equations are generally insoluble; numerical methods are the only recourse. There are unavoidable tradeoffs in terms of time, memory, accuracy, flexibility, extensibility, and robustness associated with every numerical convection scheme. Many methods have been developed, including smooth particle hydrodynamics [Monaghan, 2005] and discrete elements [Cundall and Strack, 1980]. We employ a finite elements approach [Hughes, 2012] in which the domain is divided into a discrete network of cells (the ‘mesh’): all field values are hosted on the nodes, with integrals across elements approximated using Gauss quadrature [Swarztrauber, 2003]. Such an approach can of course yield only an approximation of what the underlying equations imply, but the approximation can be arbitrarily accurate depending on the fineness of discretisation. The question, then, is how coarse can the approximation be made without losing fidelity to the governing equations?
Computationally, the problem takes the form:
Where \(A\) is the known ‘stiffness’ matrix equivalent here to viscosity, \(\overline{u}\) is a vector of unknown velocities, \(B\) is the discrete gradient operator, \(\overline{p}\) contains the pressure unknowns, \(T\) indicates the transpose, and \(\overline{f}\) is the known vector of body and boundary forces acting on the material. The objective is to solve for \(\overline{u}\) as cheaply and reliably as possible; once a velocity solution is obtained, the system can be integrated in time and the cycle begins again. First, however, we require a solution for \(p\). Multiplying both sides by \(B^TA^{-1}\) and substituting for \(B^T\overline{u}=0\) we find:
Such a form exposes the pressure to solution by a Schur Complement method, at the cost of introducing the non-trivial \(A^{-1}\) operation, which is both heavy and costly.
To avoid having to generate \(A^{-1}\), we may instead reproduce its effect using a Krylov Subspace method (KSP), wherein matrix-matrix products are resolved by decomposing them into iterative series of matrix-vector products, with each vector comprising the residual of the previous iteration until the residual is less than some nominated threshold. One very popular implementation of this concept is the Generalised Minimal Residual method, or GMRES [Saad and Schultz, 1986]. Once a solution for \(p\) is obtained, we are free to solve for \(u\) through similar methods; and this solution in turn may be used to advect the temperature field and any other state variables using a standard Petrov-Galerkin scheme; for convection problems an ‘upwind’ variant can be used to avoid ‘wiggles’ between nodes [Brooks and Hughes, 1982]. The actual time integral is carried out using a Runge-Kutta method for accuracy [Hairer et al., 2006] and is taken over a time interval chosen to be shorter than either the diffusive or the advective timescales across each element, i.e. the Courant condition [Courant et al., 1967]. Once advection has been carried out, the system is fully iterated in time and the process may be repeated, with the advantage that the pressure solution for the previous timestep can be retained to quicken the convergence of the subsequent step. Performance can be improved even further by incorporating preconditioners for each solve, which exploit a priori analytical insights into certain model configurations that may constrain the solution space [May and Moresi, 2008]
This approach is accurate, robust and stable [Moresi and Solomatov, 1995]. However, even in the best case scenario, the complexity of such a direct solution scales with the cube of the number of elements \(N^3\). To achieve a scaling behaviour closer to \(N\), it is possible to drastically reduce the workload of the inner KSPs using an adaptive multi-grid approach. With this method, a solution is obtained first for a much coarser discretisation, and then corrected over successively finer meshes until the error is within a provided tolerance. In addition to speed and resilience, the multi-grid lends itself well to parallelisation, as the first-order global features of the model can be coordinated at the coarsest levels first, while finer local features captured in heavier arrays can be shared more judiciously, thus reducing communications overheads.
The method we have outlined is the product of decades of meticulous development and is known to be as reliable as it is quick. It has been comprehensively benchmarked across a wide range of rheologies and parameters, including models with extreme viscosity contrasts [Moresi et al., 1996], elastic behaviour [Moresi et al., 2002], and strain-localising mechanisms [Moresi et al., 2007]. It has been tested against physical laboratory experiments [Mériaux et al., 2018] and has been demonstrated to be robust and scalable up to thousands of parallel processes [Farrington et al., 2005].
One shortcoming of the method we have described is the inappropriateness of the finite element mesh for preserving the geometries of integer-valued domains - for example, deformation history, or the distribution of various material phases. Though there are ways of accommodating such features using mesh-based approaches, they tend to be cumbersome and inefficient. A superior approach is to incorporate Lagrangian particle swarms [Moresi et al., 2003], which are able to carry much higher-resolution information than the mesh and can transport both real-valued data (e.g. temperature, viscosity) and integer-valued data (e.g. history, material identity), which mesh-based variables necessarily cannot. Swarms and their associated variables are advected according to the Stokes solution at the same time as the underlying mesh-based state variables. In turn, the Stokes solver calls for the swarms to be interpolated to the mesh if and when they become relevant to the solution. Interpolation can be costly and complicated for unstructured networks like particle swarms - prohibitively so if the node weightings must be recalculated with each timestep, as is the case for any advecting swarm - so it is important to carry out such an operation as infrequently and efficiently as possible. Gauss quadrature is the standard method, with simple nearest-neighbour evaluation to determine which elements own which particles. An alternative is to use a grid-based Voronoi algorithm [Velić et al., 2009] in which domains of control for each node are iteratively built out cell by cell; where two nodes lay claim to the same territory, the interpolation grid is refined, but only inside the conflicted cell, thereby minimising superfluous calculations. Another strategy, particularly suited to the interpolation of very sparse swarms, uses a k-d tree to efficiently seek out the nearest particle from any given node. Regardless of interpolation style, the addition of particle swarms dramatically extends the utility of the finite element method.
2.2.2. The Underworld code¶
Particular software implementations of the methods outlined above have been developed over many computing generations, and several continue to co-exist today as part of a broad and branching family. The present state-of-the-art iteration is Underworld, which supports 2D, 3D, multigrid, and particle-in-cell features while also combining a powerful yet modular C-level infrastructure [Quenette et al., 2007] with a user-friendly, hyper-extensible Python-based API. Parallelisation is provided through MPI while the underlying solvers are implemented with PETSc. Though deeper layers of Underworld remain fully transparent and accessible, the Python layer is designed to encourage fluidity, creativity, and legibility in model building, providing encapsulated higher-level proxies for the multifarious underlying C assets while subtly encouraging a good modelling idiom in users. This has encouraged bespoke application development [Beucher et al., 2019] and the integration of geodynamics codes with other modelling packages [Asten, 2018].
The higher-level Underworld syntax fully exploits Python’s object-oriented character, encapsulating standard model features like meshes, swarms, variables, and solvers as independent instances of generalised classes. Each object corresponds to C-level structures which are in turn organised under the StGermain interoperability framework for computational modelling [Quenette et al., 2007]. The algorithmic firepower at the heart of the operation draws on the ubiquitous standard PETSc code for partial differential equations. By default, the PETSc infrastructure is configured for robustness first, speed second; however, a range of options is exposed at the Python level to reconfigure the solvers as desired. The principles of encapsulation and localisation are carefully honoured in Underworld’s design, with use of global attributes minimised and namespace pollution strictly avoided. Consequently, deletion of obsolete references or ‘garbage collection’ operates mostly as a Python user would intuitively expect, so that in typical use cases it is rarely necessary to do more than the elementary due diligence to limit memory leaks. However, at the scales we have operated at, unavoidable pointer entropy at the C-level has been found to proliferate to problematic levels at times. This has been mitigated by prudent reuse of already instantiated objects and by spawning the heaviest or lengthiest jobs in subprocesses to harness system-level garbage collection.
As accessible as the new tools are, care must still be taken to ensure an appropriately configured model, beginning with the choice of resolution. While temporal resolution, i.e. timestep size, is determined dynamically based on the prescribed tolerances, spatial resolution is the domain of the user. Overly fine elements are wasteful, while insufficiently fine elements will lossily discretise the underlying physics. As a rule of thumb, the spatial resolution in any given region should be half an order of magnitude finer at least than the smallest relevant model features in that vicinity. Of course, it is not always clear a priori what this scale will be. Boundary layer and plume theory can provide some information about featural dimensions at steady-state for simple rheologies; however, the sensitivity of mantle convection on potentially very small-scale instabilities means a resolution sufficient for a steady-state solution may still bias the solution at other stages. The appropriate resolution can be sought empirically, by running a suite of progressively finer models until the point of diminishing returns is reached. In theory, a well-constructed model should converge with resolution in the limit that a discretised model becomes indistinguishable from a continuous one. If convergence does not occur within a computationally feasible envelope, the model may be presumed to be misconfigured in some deeper sense. Another means of determining the correct resolution is to run a single, very-high resolution test and conduct a power spectral analysis of the constituent fields; the shortest wavelength that contains information must dictate the spatial resolution. The nexus of Rayleigh number, featural thickness, and resolution places an upper bound on what parameters can realistically be tested in the context of a large suite-modelling experiment: although \(Ra\) values approaching \(10^9\) are likely more appropriate for Earth whole-mantle convection [Wolstencroft et al., 2009], most cases explored here are less than \(Ra=10^7\), which is amenable to resolutions in the order of 128 radial cells. If resources are particularly at a premium, static or even adaptive mesh refinement can be employed to concentrate resolution in areas where it is most needed. Unfortunately, it is a present shortcoming of Underworld that only quadrangular elements are supported, starkly limiting the options for grid refinement. Work toward supporting unstructured meshes is, however, underway.
Underworld provides an easy interface to the underlying PETSc options, most notably the choice of inner solve method and tolerance. The default configuration for the solver is mg or ‘multigrid’, which is the method we have outlined here: this arguably provides the best balance of speed, robustness, scalability, flexibility, and parallelisability. Alternatives include mumps, ‘multifrontal massively parallel sparse direct solver’, and the ‘lower-upper method’ LU. Careful benchmarking is called for to choose the correct configuration, and optimum results cannot be assumed for the default configuration. Tolerances in particular should always be calibrated manually using convergence and power spectrum tests as outlined above. Excessively fine tolerances will needlessly delay solver convergence, while overly generous tolerances will introduce numerical noise into the solution. The chosen tolerances ultimately determine the uncertainty inherent to the model and should always be chosen with care.
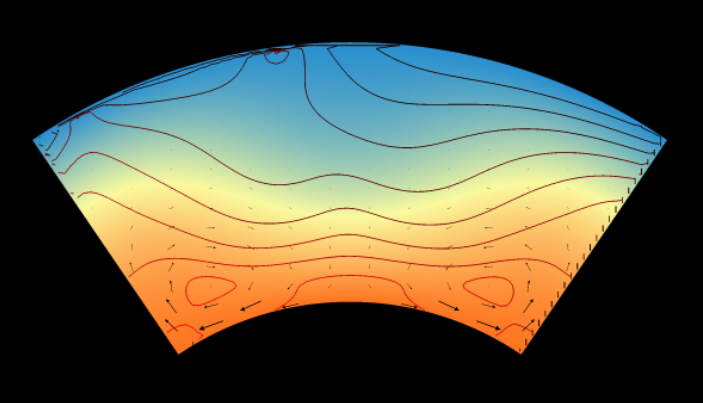
2.2.3. Underworld in the annulus¶
Even with the gift of Moore’s law, fully three-dimensional models remain prohibitively expensive, particularly at sufficient resolutions. A two-dimensional annulus is a compromise that allows exploration of the influence of curvature without exponentially expanding the degrees of freedom. Although such a geometry cannot claim to reproduce Earth-like conditions as such, it is nonetheless appropriate for probing a wide range of mantle convection phenomena and continues to be widely used.
In Underworld, which at present uses Cartesian-type meshes, the annulus is constructed by deforming a rectilinear mesh around the origin such that the ratio of inner and outer radii \(f\) falls in the range \(0\to1\), where \(f\to1\) approaches no curvature and \(f=0\) is a model with no core. When the aspect ratio and curvature are such that the two ends meet, those ends are made periodic and the result is a full annulus. For the whole Earth mantle, a ratio of \(f=0.54\) is appropriate; for the upper mantle only, a ratio of \(f = 0.9\) is more realistic. Naturally, a full annulus of \(f=1\) is not possible, while severe solver complications manifest at \(f<0.2\) due to extreme elongation of the basal cells.
Our approach to the annulus has the advantage of robustness and simplicity. It is more amenable for the solver and allows highly curved geometries without requiring a revision of any of the critical computational systems. However, it does have many shortcomings. Outer cells are stretched as inner cells are shortened, forcing a choice of either under- or over-resolution of one or other of the boundary layers. Boundary layer conditions for velocity must be defined according to unit vectors rather than simply Cartesian components; it then becomes necessary to rotate and unrotate the boundary vectors during each solver loop. In periodic cases with zero-shear upper and lower boundaries, we must also be careful to suppress any solid-body rotation that might emerge by calculating and subtracting any uniform global angular components from the velocity vector field. All of this takes time and CPU cycles, not to mention an increasingly sprawling code overhead.
For our annulus models, it has proven useful to write a bespoke mapping protocol to go from Cartesian to annular domains. The ‘box’ algorithm projects a standard unit square of \(x,y:(0,1)\) onto each annulus or annular wedge such that Cartesian positions can be smoothly and swiftly evaluated in the box and vice versa. This provides a common frame of reference between rectilinear and curvilinear models of any scale and dimensions, with benefits for interoperability, usability, and visualisation. The procedure is both parallel-safe and parallel-efficient, and approaches \(C\)-level performance through careful, idiomatic usage of the NumPy interface. In theory it could be extended to any geometry which is a continuous mapping of a rectilinear mesh.