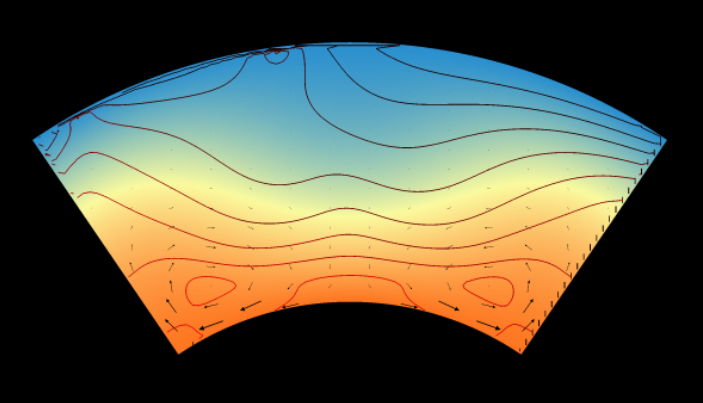
4.1. Introduction¶
Rheologies, or flow-laws, are the governing equations of any bulk fluid in motion. While it is clear that the Earth’s interior, and the interiors of the other planets, are in such a state of motion, it is not clear what rheology best describes these systems, vexing attempts to reconstruct planetary histories in the laboratory. In the thirty years since high-resolution numerical modelling became available to geodynamicists, arguably little progress has been made in designing a rheology that accurately describes geodynamic fluids on a global scale. A new approach may be called for.
Our research program seeks to test the viability of an attritional approach to planetary geodynamics based on massive and virtually complete numerical surveys of successively more complex rheologies. Rather than prematurely identifying our results with real planets or real scenarios, our approach trades immediate applicability for theoretical comprehensiveness. Once acquired, the fundamental scalings such an initiative may provide will drastically compact the possibility space for enquiries over natural systems like the silicate Earth.
For this investigation, we begin with two simple linear cases: isoviscous convection and exponentially temperature-dependent (Arrhenius-type) rheology. Across the free parameters of thermal expansivity, domain geometry, and internal heat, we sample well over 30,000 cases - a survey two orders of magnitude larger than any other known to the authors. This very large and continually growing dataset, rigorously tagged with metadata for perfect reproducibility, is put forward as a perpetual and common resource for the rheological sciences, including but not limited to our own focus of planetary geodynamics. Ultimately, the ambition of this project is to make it unnecessary for certain rheologies to ever be modelled again, and to encourage a division of labour between model production and model analysis that minimises redundant work.
In this first of two related chapters, we focus on the simpler isoviscous endmember, and focus on the scaling behaviour of the Rayleigh and Nusselt numbers across varying thermal expansivities, internal heating factors, and domain geometries. We also present a general overview of the larger dataset we are collecting and discuss the unforeseen challenges raised by, and novel solutions demanded by, a modelling effort on this scale.